Solving BVP Associated with Toroidal Geodesics

January 12, 2020

In the last post we found that the geodesics of a torus $\mathcal{T}$ were given by the following system of ODEs:

\[\begin{gathered} \theta''=\frac{2r\sin(\phi)}{R+r\cos(\phi)}\phi'\theta' \\ \phi'' = -\frac{1}{r}\sin(\phi)(R+r\cos(\phi))(\theta')^2. \end{gathered}\]

We saw that we were able to numerically solve this system if we gave an initial position and velocity for $\theta, \phi$. What we want to do now is find the geodesic between two specific points, which corresponds with solving this BVP:

\[\begin{aligned} \text{ODEs} \qquad &\left\{\begin{aligned} \theta''&=\frac{2r\sin(\phi)}{R+r\cos(\phi)}\phi'\theta' \\ \phi'' &= -\frac{1}{r}\sin(\phi)(R+r\cos(\phi))(\theta')^2. \end{aligned}\right.\\ \text{BCs} \qquad &\left\{\begin{aligned} \theta(a)&=\alpha_0 & \theta(b)&=\beta_0 \\ \phi(a)&=\alpha_1 & \phi(b)&=\beta_1 \end{aligned}\right. \end{aligned}\]

Rewriting this as a first-order system, we get

\[\begin{aligned} z_1&=\theta & &\longrightarrow z_1' = z_2 \\ z_2&=\theta' & &\longrightarrow z_2' = \frac{2r\sin(z_3)}{R+r\cos(z_3)}z_2z_4 \\ z_3&=\phi & &\longrightarrow z_3' = z_4 \\ z_4&=\phi' & &\longrightarrow z_4' = -\frac{1}{r}\sin(z_3)(R+r\cos(z_3))z_2^2 \end{aligned}\]

which can be written as the initial value problem:

\[\begin{aligned} \text{ODEs} \qquad &\left\{\begin{aligned} z_1' &= z_2 \\ z_2' &= \frac{2r\sin(z_3)}{R+r\cos(z_3)}z_2z_4 \\ z_3' &= z_4 \\ z_4' &= -\frac{1}{r}\sin(z_3)(R+r\cos(z_3))z_2^2 \end{aligned}\right.\\ \text{BCs} \qquad &\left\{\begin{aligned} z_1(a)&=\alpha_0 \\ z_2(a)&=u_1 \\ z_3(a)&=\alpha_1 \\ z_4(a)&=u_2 \end{aligned}\right. \end{aligned}\]

Solving this is slightly more difficult than an ordinary IVP, because we need 4 initial conditions, but we are only given two. We need to either find or guess $\theta’(a)$ and $\phi’(a)$. The usual elementary numerical methods that are used to solve second-order BVPs are the shooting method, and finite difference approximations. Both of these methods typically need an initial position and an initial slope, so whichever one of these methods we choose, we will still need some way of approximating $\theta’(a)$ and $\phi’(a)$, though we’ll be approaching this using the shooting method.

Let’s let $z_2(a)=u_1$ and $z_4(a)=u_2$ (remember that in our formulation above, $z_2(t)=\theta’(t)$, and $z_4(t)=\phi’(t)$). We can think that whatever values we choose for $u_1,u_2$ will determine the angle that we will “shoot” from, which will then determine our final position. We want to choose $u_1$ and $u_2$ such that $z_1(b)=\beta_0$ and $z_3(b)=\beta_1$. Therefore $z_1(b)$ and $z_3(b)$ are dependent on $u_1$ and $u_2$, which we can express as

\[\begin{aligned} z_1(b) &= g_1(u_1, u_2) \\ z_3(b) &= g_2(u_1, u_2). \end{aligned}\]

We should choose $u_1, u_2$ such that

\[\begin{aligned} g_1(u_1, u_2) &= \beta_0 \\ g_2(u_1, u_2) &= \beta_1 \end{aligned}\]

or written another way,

\[\begin{aligned} g_1(u_1, u_2) - \beta_0 &= 0 \\ g_2(u_1, u_2) - \beta_1 &= 0, \end{aligned}\]

which is now a root finding problem! We don’t actually know analytic forms for $g_1$ or $g_2$, but that’s okay because we’ll be approximating them.

To begin our solution, we need initial guesses for $u_1,u_2$. There are probably more sophisticated ways to approach this, but a secant approach such that $u_1=\frac{\beta_0-\alpha_0}{b-a}$ and $u_2=\frac{\beta_1-\alpha_1}{b-a}$ should give acceptable enough convergence. The Newton-Raphson method is notorious for being extremely sensitive to initial conditions, meaning that it may converge quickly for some initial condition a, but diverge for some perturbation a+$\delta$, so it may be helpful to put more thought into our initial guess. More on this later.

So how does this algorithm work? To start, we use RK45 with initial conditions $\left[\alpha_0, \frac{\beta_0-\alpha_0}{b-a}, \alpha_1, \frac{\beta_1-\alpha_1}{b-a}\right]$. This gives us approximations for $z_1(b)=g_1(u_1,u_2)$ and $z_3(b)=g_2(u_1,u_2)$. We can then construct our residual function by letting

\[x=\begin{bmatrix}u_1\\u_2\end{bmatrix} \quad \text{and} \quad F(x)=\begin{bmatrix}g_1(u_1, u_2) - \beta_0\\ g_2(u_1, u_2) - \beta_1\end{bmatrix}.\]

We then solve $F(x)=0$ using Newton-Raphson, which gives us approximate values $z_2(a)$ and $z_4(a)$. The Newton-Raphson method takes care of the shooting part of the algorithm, because if our initial guess for $u_1,u_2$ did not produce an approximation within an acceptable tolerance, it will choose a new $u_1’,u_2’$ using the Jacobian of $F(x)$, use that as the new input for RK45, get new approximations for $g_1’(u_1’, u_2’),g_2’(u_1’,u_2’)$, and then try to find the root for that. The MATLAB code is located in this gist. There’s also more details about solving this style of ODE in Chapter 5 of Boundary Value Problems for Engineers with MATLAB Solutions¹ by Keskin.

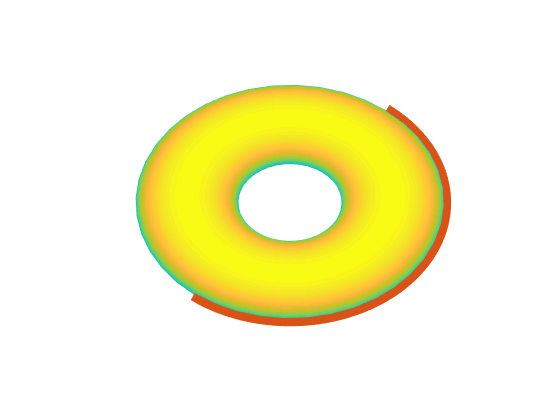
Let’s look at some examples. We want to find the geodesic between points $(0,0)$ and $(0,\pi)$. I have assumed that $r=1$ and $R=2$, and also that $a=0,b=1$. This assumption of $t\in[0,1]$ isn’t actually based on any intuition, which comes back to bite us later. For now, let’s just assume that this is a sufficient enough span for $t$.

\[\begin{aligned} \text{ODEs} \qquad &\left\{\begin{aligned} \theta''&=\frac{2\sin(\phi)}{2+\cos(\phi)}\phi'\theta' \\ \phi'' &= -\sin(\phi)(2+\cos(\phi))(\theta')^2 \end{aligned}\right.\\ \text{BCs} \qquad &\left\{\begin{aligned} \theta(0)&=0 & \theta(1)&=\pi \\ \phi(0)&=0 & \phi(1)&=0 \end{aligned}\right. \end{aligned}\]

Let’s think about what our solution should look like. We know $\theta$ should start at $0$ and end at $\pi$, so it should rotate along the upper half of the torus. And because $\phi$ starts and ends at $0$, it should remain constant. Below is an image showing the solution, which matches our intuition. The initial approximations for the slopes ended up being $\theta’(a) \approx 3.141592653589793$ and $\phi’(a) \approx 0$.

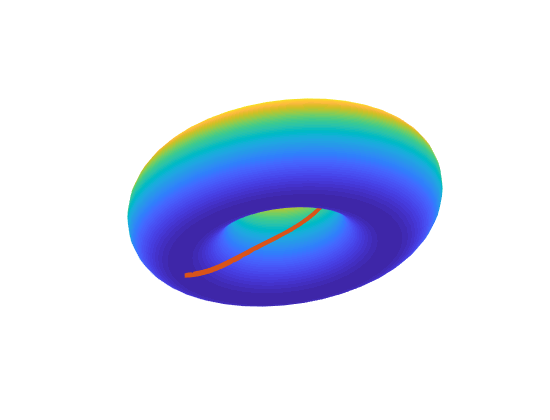
Here’s another cool one that is a solution to

\[\begin{aligned} \text{ODEs} \qquad &\left\{\begin{aligned} \theta''&=\frac{2\sin(\phi)}{2+\cos(\phi)}\phi'\theta' \\ \phi'' &= -\sin(\phi)(2+\cos(\phi))(\theta')^2 \end{aligned}\right.\\ \text{BCs} \qquad &\left\{\begin{aligned} \theta(0)&=0 & \theta(1)&=\pi \\ \phi(0)&=\frac{\pi}{2} & \phi(1)&=\frac{3\pi}{2} \end{aligned}\right. \end{aligned}\]

I ran into a problem when trying to solve this particular formulation:

\[\begin{aligned} \text{ODEs} \qquad &\left\{\begin{aligned} \theta''&=\frac{2\sin(\phi)}{2+\cos(\phi)}\phi'\theta' \\ \phi'' &= -\sin(\phi)(2+\cos(\phi))(\theta')^2 \end{aligned}\right.\\ \text{BCs} \qquad &\left\{\begin{aligned} \theta(0)&=0 & \theta(1)&=\pi \\ \phi(0)&=\frac{\pi}{2} & \phi(1)&=\frac{\pi}{2} \end{aligned}\right. \end{aligned}\]

When I first tried to solve using the method above, it failed. Initially I thought it was because my Newton-Raphson implementation would stop after a maximum of $100$ iterations. I tried to mitigate this problem by raising the number of max iterations to $250$ to see if it would then converge, but it still failed. Then I thought that the initial guess of of $[\pi, 0]$ for $[u_1,u_2]$ (which was obtained from the secant approximation discussed above) was causing the slow convergence. So I attempted the algorithm with some more random initial values like $[1,1]$, but it still did not converge.

The solution to this convergence problem was that it was unable to find a geodesic in the interval $[a,b]$. I had been using $a=0,b=1$ for all of my testing and the method converged for all starting points that I had tried. But once I tried $\left(0, \frac{\pi}{2}\right)$ and $\left(\pi, \frac{\pi}{2}\right)$, it failed. I suppose this is because as $t$ spanned this interval, it didn’t have enough “length” to reach the terminal point $\left(\pi, \frac{\pi}{2}\right)$. I’m not sure what causes the method to fail, or if there is some analytical way to determine if the method is going to fail given the initial point, the terminal point, and the span of $t$. Either way, changing the interval of $t$ from $[0,1]$ to $[0,5]$ gave quick convergence.

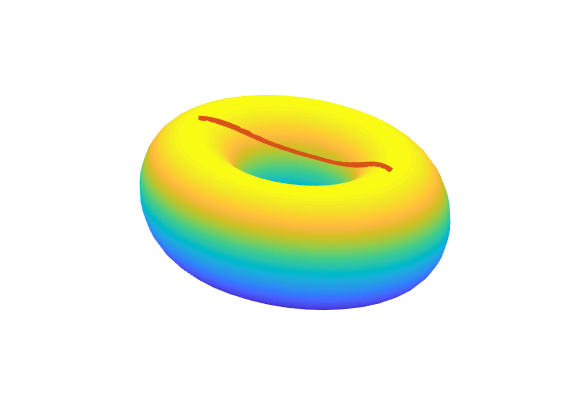
I also found that $[0,4.5]$ worked, so there must be some tolerance in the choice for the span of $t$, but I’m going to have to explore this issue further. Allegedly these types of unknown boundary value problems or free boundary value problems, where the value of $b$ is unknown, come up a lot in engineering. There is a way to solve these problems with something called the reverse shooting method, but I’ve only seen this method employed for single ODEs, not coupled ones like we’re dealing with. Essentially the divergence could be caused by any combination of these factors:

1. Arbitrary $b$ value being used instead of analytically or numerically finding a suitable $b$.
2. Newton-Raphson is not robust enough to tackle this kind of problem, and instead something more reliable like MATLAB’s fsolve should be used.
3. Initial guess using secant method is not accurate enough (although this is more of a problem with the fragility of N-R). It may be better to employ Newton’s method over the secant method here for a more accurate guess.

---